이번 게시글에서는 6면체 주사위 n 개를 던져 그 합의 분포를 구하는 실험을 10,000번 시행해보고자 한다. 손으로 던질껀 아니고, Python을 통해 시뮬레이션 해 볼 예정이다.
이론적으로 면이 6개인 단일 주사위를 한 번 던졌을 때 기대값은 $\frac{1+2+3+4+5+6}{6} = \frac{7}{2}$이다.
확률이 $p$인 사건을 $n$번 시행하여 사건 발생 횟수에 따른 확률을 구하면, 그것을 확률 $p$, 시행횟수$n$인 이항분포라고 정의하고 $B(n,p)$로 표현하며, 평균은 $np$, 분산은 $np(1-p)$임이 잘 알려져 있다. 1개 6면체 주사위를 던졌을 때 평균이 $np = \frac{7}{2}$ 이고, 확률은 $\frac{1}{6} $이므로, 분산은 $\frac{7}{2} (1-\frac{1}{6}) = \frac{35}{12} $ 이다.
또, 드무아브르-라플라스 정리에 따르면, 시행횟수 N이 충분히 클 때 이항분포 $B(n,p)$는 정규분포 $N(np, np(1-p)$와 같아진다. 따라서 주사위 $n$개를 던져서 나오는 합의 분포는 정규분포 $N( n*\frac{7}{2} , \sqrt{n*(\frac{35}{12})}$를 근사적으로 따를 것이다.
드무아브르-라플라스 정리는 중심극한정리의 특별한 경우이다. 중심극한정리에 대한 간략한 설명이 궁금한 사람은 아래 더보기 버튼을 눌러보자.
중심극한정리는 간단히, 많은 독립 확률변수의 합이 근사적으로 정규분포를 따른다는 것이다. 이 정리는 독립확률변수의 합에 대한 근사적인 확률을 계산하는 간단한 방법을 제공할 뿐 아니라, 대부분의 자연적인 모집단의 경험 도수들이 정규분포를 나타낸다는 주목할만한 사실을 설명하는데 도움이 된다.
$X_1, X_2, X_3, \cdots , X_n $은 일련의 도립이며 각각 평균이 m이고 분산이 $\sigma^2$ 인 동이랗게 분포된 확률변수라고 하자. 그러면,
$$ \frac{X_1+\cdots+X_n - nm}{\sigma\sqrt{n}} $$
의 분포는 $n\to \infty$일 때 표준정규분포에 수렴한다. 즉,
$$ P[\frac{X_1 + \cdots + X_n - nm}{\sigma\sqrt{n}}\leq a] \to \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{a} e^{-x^2/2}dx $$
중심극한정리에 따르면, 평균이 $m$, 분산이 $\sigma^2$인 모집단에서 n개의 표본을 뽑아서 계산한 표본평균$ \tilde{X}$는 $n$이 커질 때 $N (m,\frac{sigma^2}{n})$을 따른다. 표본평균의 분산이 원래 모집단 분산을 $n$으로 나눈 값이 된다는 것은, $n$이 커질수록 표본평균의 분산이 점점 0에 가까워지게 되어, 표본평균을 실제 평균으로 간주해도 문제가 없게 된다는 것이다. 다시 말하면, 동일분포를 가지는 분포들의 평균은 개수가 많아지면서 언제나 정규분포로 수렴한다.
아무튼, 주사위 2개를 던져서 나오는 합의 분포는 정규분포 $N(7,\sqrt{\frac{35}{6}})$를, 주사위를 3개 던져서 나오는 합의 분포는 정규분포$N(\frac{21}{2},\sqrt{\frac{35}{4}})$를, 주사위 12개를 던져서 나오는 합의 분포는 정규분포 $N(42,\sqrt{35})$ 를 따를 것으로 예상된다. 각각에 해당되는 (이론적)분포 그래프는 다음과 같다.
못 믿겠다면, 직접 일일이 구해봐도 무방하다. 주시위 2개를 굴릴 때만 해보면,
| 합 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 확률 | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
그래프는 다음과 같을 것이다.
자, 이제 본격적으로 실험을 진행해보자. 코드는 아래와 같다. 환경은 Google Colab.기준이다.
!pip install chart_studio먼저 pyplot을 사용하기 위해 chart_studio를 깔아준다. 물론 더 편한 matplotlib이나 seaborn과 같은 패키지도 있지만, pyplot만큼 이쁘지 않은 것 같아서, Pyplot을 애용한다. matplotlib을 사용해 그리는 방법은 인터넷에 많으니 참고하면 좋을 것 같다.
import numpy as np
import chart_studio
chart_studio.tools.set_credentials_file(username='username',api_key='api_key')
import plotly.graph_objects as go
from plotly.offline import iplot, init_notebook_mode
from scipy.stats import norm다음 필요한 package를 불러오고,
def configure_plotly_browser_state():
import IPython
display(IPython.core.display.HTML('''
<script src="/static/components/requirejs/require.js"></script>
<script>
requirejs.config({
paths: {
base: '/static/base',
plotly: 'https://cdn.plot.ly/plotly-1.5.1.min.js?noext',
},
});
</script>
'''))
configure_plotly_browser_state()
init_notebook_mode(connected=False)Pyplot을 Colab. notebook에서 직접 볼 수 있게끔 해주는 script를 실행시켜준다. 업데이트가 되었는지 위의 스크립트 없이도 제대로 notebook내에서 render되는 경우도 있는데, 안되는 경우도 있어서 그 경우 입력해주자. Google Colab.에서 Plotly를 Display하고, html로 저장하는 방법 글 참고.
다음, scipy에 포함된 norm 함수를 이용해 정규분포를 따르는 data를 만들어준다.
dice2= norm(7,(35/6)**0.5).pdf(np.arange(-5,20,0.1))
dice3= norm(21/2,(35/4)**0.5).pdf(np.arange(-5,30,0.1))
dice12= norm(42,35**0.5).pdf(np.arange(0,80,0.1))더 많은 dice에 대해서 실험하고자 한다면, for문을 사용해 좀 더 유려하게 만들수도 있겠다. 이번엔 3개만 확인할거라서 패스.
마지막으로 그래프를 작성해준다.
fig=go.Figure()
fig.add_trace (go.Scatter(x=np.arange(-5,20,0.1),y=dice2,mode='lines',name='N(7,2.41)'))
fig.add_trace (go.Scatter(x=np.arange(-5,30,0.1),y=dice3,mode='lines',name='N(10.5,2.95)'))
fig.add_trace (go.Scatter(x=np.arange(0,80,0.1),y=dice12,mode='lines',name='N(42,5.91)'))
fig.update_layout(title={'text': 'Theoretical distribution for n dice', 'y':0.9,'x':0.5, 'xanchor': 'center', 'yanchor' : 'top'})
iplot(fig)Out>
각각 따로 살펴보면 다음과 같은 모양이다.
이제 본격적으로 주사위를 프로그램적으로 만들어서 진짜 저런 분포가 되는지 실험해보자. 주사위는 던지면 1~6사이의 숫자가 random하게 나와야 한다. Python에는 가장 기본적인 random package에서도 잘 제공하고 있다. 그런데 과연 python의 random package에 있는 random이 진짜 'random'인지 궁금해 할 수 있다. 어쨌거나 어떤 임의의 알고리즘을 걸쳐서 뽑는 숫자인데, 이게 Random이라고 할 수 있을까? 그 답은 '진짜 Random은 아니다.'이다. 따라서 이를 '유사난수 발생기' 라고 한다. 그렇지만, 현재는 거의 Random에 가까운 MT19937(Mersenne Twister 19937) 알고리즘을 현재 사용하고 있다. 예~전에 사용하던 Linear congruential generator보다 발전된 형태이다. MT19937은 난수의 반복 주기가 메르센 소수인 $2^{19937}-1$ 이며, 생성된 난수는 623차원까지 동일분포되어있다고 한다. 그러므로, 우리 실험을 진행하는 데 있어서 큰 문제는 없다.
Python의 random package를 사용해도 좋지만, 앞에서 이미 numpy package를 불러왔으니까 numpy에 있는 random을 사용해서 주사위를 구현해보았다. 다음 코드를 보자.
die=np.random.randint(1,7,size=size)이렇게 하면 1부터 7까지의 숫자를 size 만큼 뽑아준다. 단 한줄의 코드로 n번 시뮬레이션 해주는 것이다. 이제 주사위를 두 개 만들어서, 그 합을 히스토그램 분포로 나타내고 이론적으로 구한 값과 비교해볼것이다. 그리고 주사위는 10번, 100번, 1,000번, 10,000번 던져서 시행횟수에 따른 변화를 같이 살펴볼 것이다.
먼저 주사위 두 개로 시작하자.
fig_2dice = go.Figure()
fig_2dice.add_trace (go.Scatter(x=np.arange(-5,20,0.1),y=dice2,mode='lines',name='N(7,2.41)'))
for i in range(1,5,1):
size=10**i
die1=np.random.randint(1,7,size=size)
die2=np.random.randint(1,7,size=size)
diesum = die1 + die2
fig_2dice.add_trace (go.Histogram(x=diesum,histnorm='probability',name=f'roll {size} times' ))
fig_2dice.update_layout(title={'text': 'Theoretical vs experiment Distribution for couple of dice', 'y':0.9,'x':0.5, 'xanchor': 'center', 'yanchor' : 'top'})
configure_plotly_browser_state()
init_notebook_mode(connected=False)
iplot(fig_2dice)Out>
하나씩 살펴보면 다음과 같다.
시행 횟수가 10번일때는 분포와 거의 맞지 않지만, 시행횟수가 늘어날수록 실험적 분포가 이론적 분포에 가까워지는 것을 확인할 수 있다. 주사위가 세개일때와 열두개일때는 어떨까?
주사위 세개일때는 다음과 같다.
fig_3dice = go.Figure()
fig_3dice.add_trace (go.Scatter(x=np.arange(-5,30,0.1),y=dice3,mode='lines',name='N(10.5,2.95)'))
for i in range(1,5,1):
size=10**i
die1=np.random.randint(1,7,size=size)
die2=np.random.randint(1,7,size=size)
die3=np.random.randint(1,7,size=size)
diesum = die1 + die2 + die3
fig_3dice.add_trace (go.Histogram(x=diesum,histnorm='probability',name=f'roll {size} times' ))
fig_3dice.update_layout(title={'text': 'Theoretical vs experiment Distribution for Tirpe dice', 'y':0.9,'x':0.5, 'xanchor': 'center', 'yanchor' : 'top'})
configure_plotly_browser_state()
init_notebook_mode(connected=False)
iplot(fig_3dice)Out>
각 시행횟수 vs 이론적 분포는 다음과 같다.
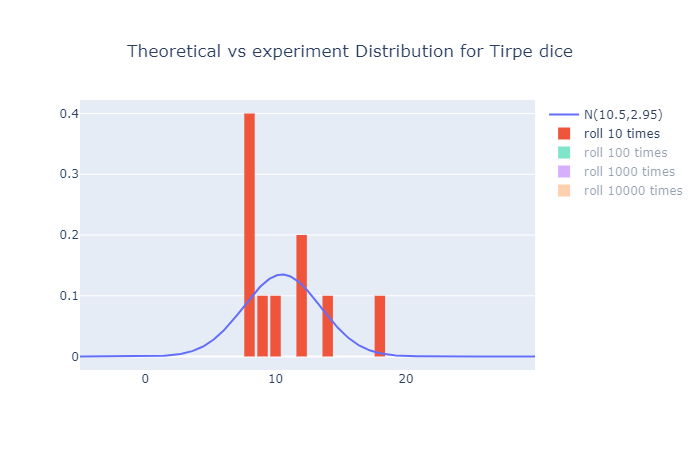
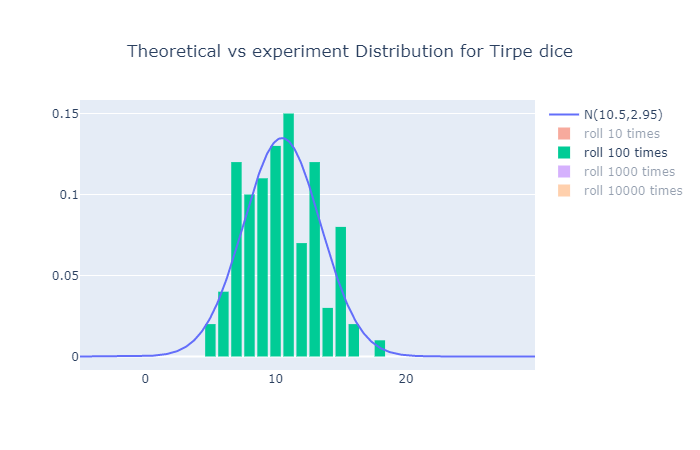
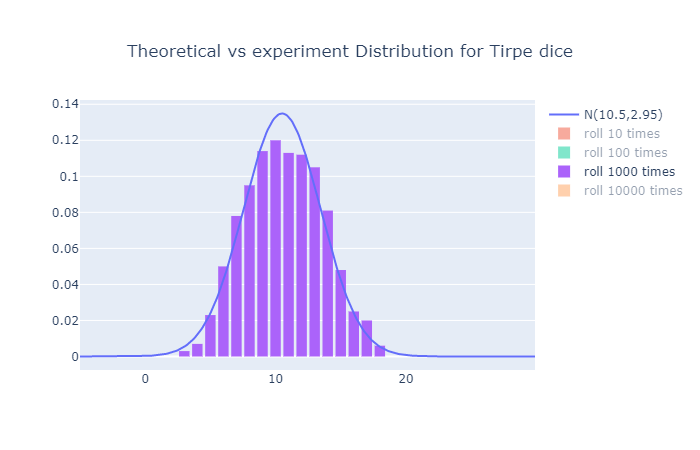
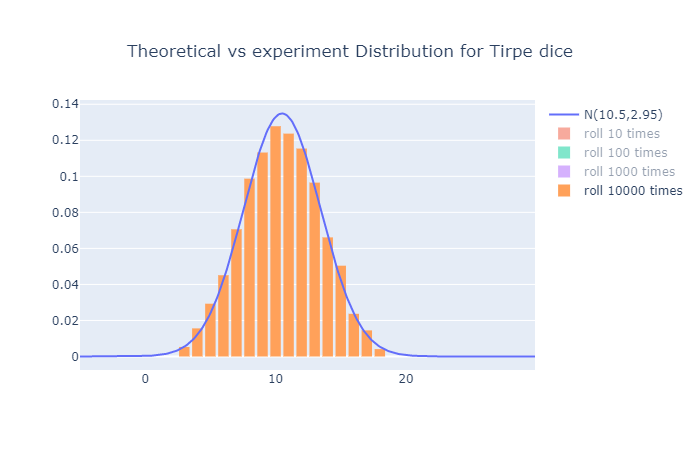
역시나 시행횟수가 많아질수록 이론값에 접근하는 모습이다.
마지막으로 12개일 때이다.
fig_12dice = go.Figure()
fig_12dice.add_trace (go.Scatter(x=np.arange(0,80,0.1),y=dice12,mode='lines',name='N(42,5.91)'))
for i in range(1,5,1):
size=10**i
die1=np.random.randint(1,7,size=size)
die2=np.random.randint(1,7,size=size)
die3=np.random.randint(1,7,size=size)
die4=np.random.randint(1,7,size=size)
die5=np.random.randint(1,7,size=size)
die6=np.random.randint(1,7,size=size)
die7=np.random.randint(1,7,size=size)
die8=np.random.randint(1,7,size=size)
die9=np.random.randint(1,7,size=size)
die10=np.random.randint(1,7,size=size)
die11=np.random.randint(1,7,size=size)
die12=np.random.randint(1,7,size=size)
diesum = die1 + die2 + die3 + die4 + die5 + die6 + die7 + die8 + die9 +die10 +die11 + die12
fig_12dice.add_trace (go.Histogram(x=diesum,histnorm='probability',name=f'roll {size} times' ))
fig_12dice.update_layout(title={'text': 'Theoretical vs experiment Distribution for 12 dice', 'y':0.9,'x':0.5, 'xanchor': 'center', 'yanchor' : 'top'})
configure_plotly_browser_state()
init_notebook_mode(connected=False)
iplot(fig_12dice)Out>
코드에 대해서 조금의 변명 부연설명을 하자면 이렇게 복붙 노가다를 한 이유는, 직관적으로 나타내기 위해서다. 절대 절대 귀찮아서가 아니다.
마지막 그래프는 사진으로 비교하지 않고, 하단에 첨부한다. 직접 비교해보시라. 그래프에 커서를 올리면 interaction할 수 있다. Legend를 하나씩 골라 이론값과 비교해보자.
역시나 시행횟수가 커지면서 이론적 값에 실제로 접근하는 것을 실험적으로 확인할 수 있었다.
이번 간단한 실험을 통해 n개 6면체 주사위의 합을 구하는 것이 중심극한정리를 따르며, 시행횟수가 커지면서 실사건의 확률이 통계적 예측에서 오차가 줄어감을 확인할 수 있었다. (이를 큰 수의 법칙이라고 한다.)
다음번에 기회가 된다면, N면체 주사위의 합의 분포는 어떻게 될 지 분석해보겠다.
아래는 이번 실험 코드가 담긴 Colab. 주소이다.
http://colab.research.google.com/drive/1o-GNFFH5f5k76MxUaPcxcjIwKukuHA9M?usp=sharing
Google Colaboratory
colab.research.google.com
