축구공의 꼭지점은 몇개일까?

축구공은 위 사진처럼 가운데 오각형 1개가 있고 이를 6각형 5개가 감싸고 있는 패턴이 반복된다. 또, 꼭지점들을 살펴보면 모든 꼭지점이 6각형 2개, 5각형 1개로 상황이 같다.
이 경우 볼록다면체 데카르트 정리를 사용해 꼭지점의 개수를 구할 수 있다. 볼록다면체 데카르트 정리는 다음과 같이 요약할 수 있다.
"꼭지점에서 손실각을 합하면 $4\pi$ 이다."
이 때 손실각은 $360^{\circ}-$한 점에 모여있는 다각형들의 그 점에서의 각의 합 으로 정의된다.
예를들어 다음 정육면체를 생각해보자.

왼쪽 정육면체의 표시된 꼭지점은 주변에 90도 3개를 가지고 있으므로, 손실각은
$$ 360^{\circ} - (90^{\circ} \times 3) = 90^{\circ} = \frac{\pi}{2} \ rad$$
따라서 손실각의 총합은 도형 꼭지점 개수 $\times$ 꼭지점 당 손실각 이므로, 이 도형의 꼭지점 개수는
$$ \frac{4\pi}{2/\pi} = 8$$
8개 인 것을 알 수 있다.
두번째 예시로, 정사면체를 살펴보자.
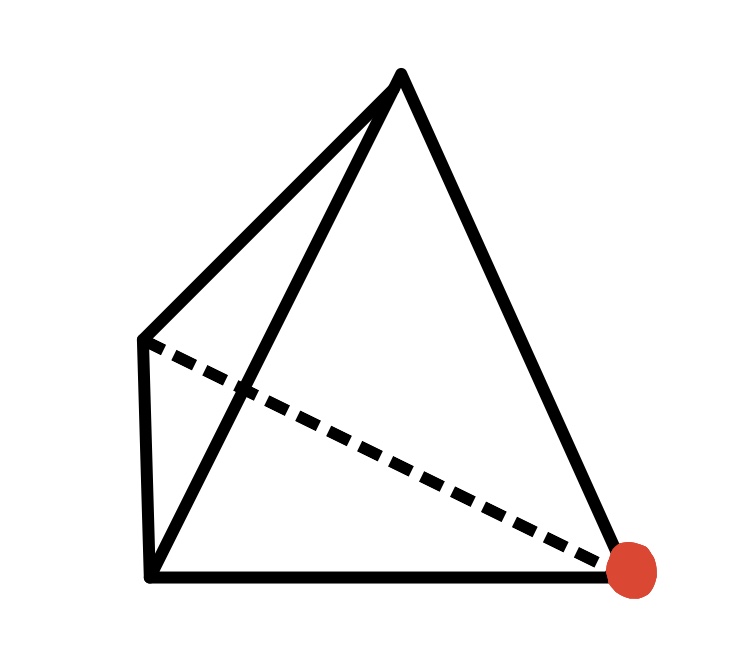
왼쪽 정사면체에 표시된 꼭지점에서 손실각은
$$ 360^{circ} - (60^{\circ} \times 3) = 180^{\circ} = \pi$$
따라서 이 도형의 꼭지점 개수는
$$ \frac{4\pi}{\pi} = 4$$
4개인 것을 알 수 있다.
자 이제, 우리가 원래 구하려고 했던 축구공의 꼭지점 개수를 구해보자. 축구공 한개의 점에는 육각형 두개와 오각형 한개가 모여있음을 이용해서 손실각을 구하면,
$$360^{\circ} - (120^{\circ} \times 2 + 108^{\circ}) = 12^{\circ} = \frac{\pi}{15}$$
이므로, 축구공 꼭지점 개수는
$$\frac{4\pi}{\pi/15} = 60$$
60개가 됨을 쉽게 구할 수 있다.
