1. 회절(Diffraction)
회절(Diffraction)은 빛이 진행하면서 직진성이 깨지는 현상이다. 우리가 무한히 작은 빛, 혹은 퍼지지 않는 빛을 만들 수 없는 이유가 바로 회절 때문이다. 회절과 비슷한 용어로 '간섭(Interference)'을 들어보았을 것이다. 회절과 간섭은 사실 같은 현상이다. 간섭은 유한개의 파동이 중첩될 때, 회절은 수 많은 파동이 중첩될 때 에너지 분포가 달라지는 현상을 회절이라고 한다. 일상생활에서 경험하는 회절 사례로는 통신이 있다. 회절이 잘 일어나기 위해서는 장애물 크기와 파장의 order 가 비슷해야한다. 파장이 장애물의 길이에 비해 짧으면 회절이 잘 일어나지 않는다. 전파망원경은 회절의 원리를 역이용한 것으로, 우주로부터 오는 라디오파 신호를 평면파로 가정해 각 안 테나로 보강간섭이 일어나는 곳에서 신호를 $𝑁^2$으로 증폭하여 수신한다. 따라서 안테나 사이의 거리는 측정 코자 하는 전자기파의 파장 조건에 맞추어져 있다. 예를 들어, 오스트레일리아 전파망원경은 수소 방출 스펙트럼 21cm을 측정하기 위해 32개 전파망원경 사이 거리를 7m로 두었다.
2. Huygens-Frsenel (호이겐스-프레넬) 원리
1차 파면상의 각 점이 독립적인 구면파의 소스가 된다는 Huygen's principle은 빛의 직진성을 설명하며 파면을 설명했으나, 진폭 및 파장 의존도는 설명하지 못했다. (이 게시물을 참조) Huygen's principle를 바탕으로 Fresnel은 진행하는 파면의 막히지 않은 모든 점은 2차 구면파의 소스(source)가 되며, 이 때 2차 파동의 진폭은 생성된 점광원 구면파들의 중첩에 의해 결정된다는 것을 즉, 위상을 고려해야한다는 것을 발견했다. 이를 Huygens-Fresnel's principle 라고 한다.
예를 들어, 파장이 𝜆인 파동이 길이 𝑎의 슬릿을 통과한다고 가정하자. 그럼 이 슬릿상의 모든 구멍은 각각 2차 구면파의 source가 된다는 것이다. 그리고 각 점광원에서 퍼진 구면파의 중첩으로 진폭과 위상이 결정된다. 따라서 파장의 길이와 슬릿의 길이가 중요하다. 만약 𝜆 ≪ 𝑎 일 때에는 중심에서 조금만 벗어나도 상쇄 간섭이 일어나 회절이 잘 일어나지 않는다. 반대로 𝜆 ≫ 𝑎 일 때에는 구멍 뒤 대부분의 위치에서 보강간섭이 일어나므로 회절이 강하게 일어난다. Slit의 간격이 줄어들수록 점광원과 같이 회절이 아주 잘 일어나게 된다.
회절이 호이겐스-프레넬 원리에 의해 발생하기 때문에, 슬릿으로부터 거리에 따라 회절에 의한 파면의 모양이 달라지게 된다. 슬릿으로부터 가까운 위치에서는 퍼짐이 적고 파면의 모양은 복잡하지만, 멀어지면 충분한 중첩이 이루어져 보다 간단한 모양을 갖는다. 슬릿과 가까운 곳에서 만들어지는 회절모양을 Fresnel diffraction (프레넬 회절) 또는 near-field diffraction 이라고 하고, 슬릿에서 먼 위치에서 만들어지는 회절을 Fraunhofer diffraction (프라운호퍼 회절) 혹은 far-field diffraction 이라고 한다. 우리가 회절을 계산할 때는 주로 Fraunhofer 회절이 발생할 때 근사적으로 계산한다. 슬릿에서 파면까지의 길이를 $R$ 이라고 하면 Fraunhofer diffraction은 다음 조건을 갖는다.
$$R>a^2/\lambda$$
 |
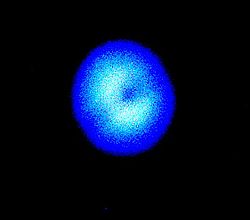 |
| Computer simulation of Fraunhofer diffraction by a rectangular aperture | Fresnel diffraction showing central Arago spot |
image from wikipedia.org
3. 회절의 계산
한편, 회절을 정확하게 계산하는 것은 쉽지 않다. 보통 전자기파의 전파식에 바탕을 두고 근사적으로 계산한다. 슬릿상에 N개의 구멍이 있을 때, 스크린에 중첩되는 전기장은 아래와 같이 계산할 수 있다.

대괄호 안의 값은 등비 수열이므로, 아래와 같이 정리할 수 있다.
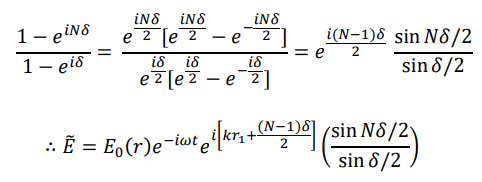
이 때 $R = \frac{1}{2} (N-1)d sin \theta + r_1 $ 으로 정의하면,

따라서 빛의 세기 $I$ 는

로 구할 수 있다. 즉, $\delta = \frac{2\pi}{\lambda} d sin \theta$이므로 $d sin \theta = m \lambda (m=0,\pm 1, \pm 2, ... )$ 일 때, $I = N^2 I_0$ 가 되어 가장 회절 세기가 커진다. 회절 각도가 커질수록 빛의 세기는 작아지며, $\frac{N\delta}{2} = \pi$ 일 때 $I$ 는 첫 번째 최솟값이자 0이 된다. $sin\theta <=1$ 이기 때문에 $d<\lambda$ 이면 (파장이 너무 길면) 회절 모양은 최대값 $N^2 I_0$만 존재하고 최소값은 존재하지 않게 된다.


