편광은 아주 중요한 빛의 특성이다. 우리가 빛을 이용해 다양하게 사용할 수 있는 것도 바로 편광 덕분이다. 편광은 빛의 진동 상태이다. 조금 더 구체적으로 기술하자면, 전기장의 시간 또는 공간에 따른 진동상태를 편광이라고 한다. 만약 전기장의 진동방향이 시공간에 상관없이 일정하다면 선형편광이라고 하며, 진동하는 방향을 포함해 진동방향에 수직한 평면을 진동 방향이라고 한다. 선형 편광 이외에도 원형 편광, 타원편광이 있다. 하나씩 알아보자.
1. 선형편광 (linear polarization)
여기 서로 수직한 방향으로 진동하는 두 전기장이 있다.
$$ \vec{E_x}(z,t) = \hat{i} E_{0x}cos(kz-\omega t) $$
$$ \vec{E_y}(z,t) = \hat{j} E_{0y}cos(kz-\omega t + \varepsilon) $$
이 때 $\varepsilon$은 $x$값에 대한 상대적 위상차이다. $z$축을 따라 진행하는 임의의 전자기파는
$$ \vec{E} (z,t) = \vec{E_{x}} + \vec{E_y} $$
만약 두 전기장의 위상차 $\varepsilon$이 0 또는 $2\pi$ 만큼 차이난다면,
$$ \vec{E}(z,t) = (\hat{i}E_{0x} +\hat{j}E_{0y})cos(kz-\omega t)$$
가 된다. 즉, 최종 전기장이 고정된 진폭 $(E_{0x} +E_{0y} = E_0)$을 가지고 진동을 한다. 이를 선형편광되어있다고 한다. 만일 두 전기장의 위상차 $\varepsilon$이 $\pi$만큼 차이가 난다면,
$$ \vec{E}(z,t) = (\hat{i}E_{0x} + \hat{j}E_{0y}) cos (kz-\omega t) $$
역시 고정된 진폭을 가지며 선형 편광 되어있다.
2. 원형 편광 (Circular polarization)
이번에는 두 전기장의 위상차가 $\varepsilon = -\frac{\pi}{2} + 2m\pi \ (m=0,\pm1,\pm2,cdots) $ 만큼 차이 난다고 가정하자. 그렇다면 전기장은,
$$ \vec E = E_0[\hat{i}cos(kz-\omega t)+\hat{j}sin(kz-\omega t)] $$
즉, 전기장의 크기는 $E_0$로 일정하고 방향이 계속 변한다. 이 때 $x$성분이 $y$성분보다 $\frac{\pi}{2}$ 앞서고 있으므로, 반시계방향으로 회전한다. 이와 같은 편광 상태를 우원편광 (right-circularly polarization) 이라고 한다.
만약 두 전기장의 위상차가 $\varepsilon = \frac{\pi}{2} + 2m\pi \ (m=0,\pm1,\pm2,\cdots) $ 라면 전기장은,
$$ \vec E = E_0[\hat{i}cos(kz-\omega t)-\hat{j}sin(kz-\omega t)] $$
이 되고 전기장의 크기는 역시 $E_0$로 일정하면서 $y$성분이 $x$성분보다 \frac{\pi}{2} 만큼 앞서므로 시계방향으로 회전하고 좌원편광(left-circularly polarization)이라고 한다.
3. 타원 편광 (eplliptic polarization)
만약 두 전기장의 위상차$\varepsilon$가 선형편광, 혹은 원형편광이 될 조건이 아닌 임의의 어떤 값이 되면 그 전기장을 타원 편광상태라고 한다. 그러므로 선형편광과 원형편광은 타원편광의 특수한 경우라고 볼 수 있다. 타원편광 상태일 때 일반적으로 전기장의 크기는
$$ (\frac{E_y}{E_{0y}})^2 + (\frac{E_x}{E_{0x}})^2 - (\frac{E_x}{E_{0x}})(\frac{E_y}{E_{0y}})cos\varepsilon = sin ^2 \varepsilon $$
이 되는데, 위 방정식은 타원방정식이고 장축이 $x$축과 이루는 각도 $\alpha$는 다음과 같다.
$$ tan 2\alpha = \frac{2E_{0x}E_{0y}cos\varepsilon}{E_{0x}^2 - E_{0y}^2} $$
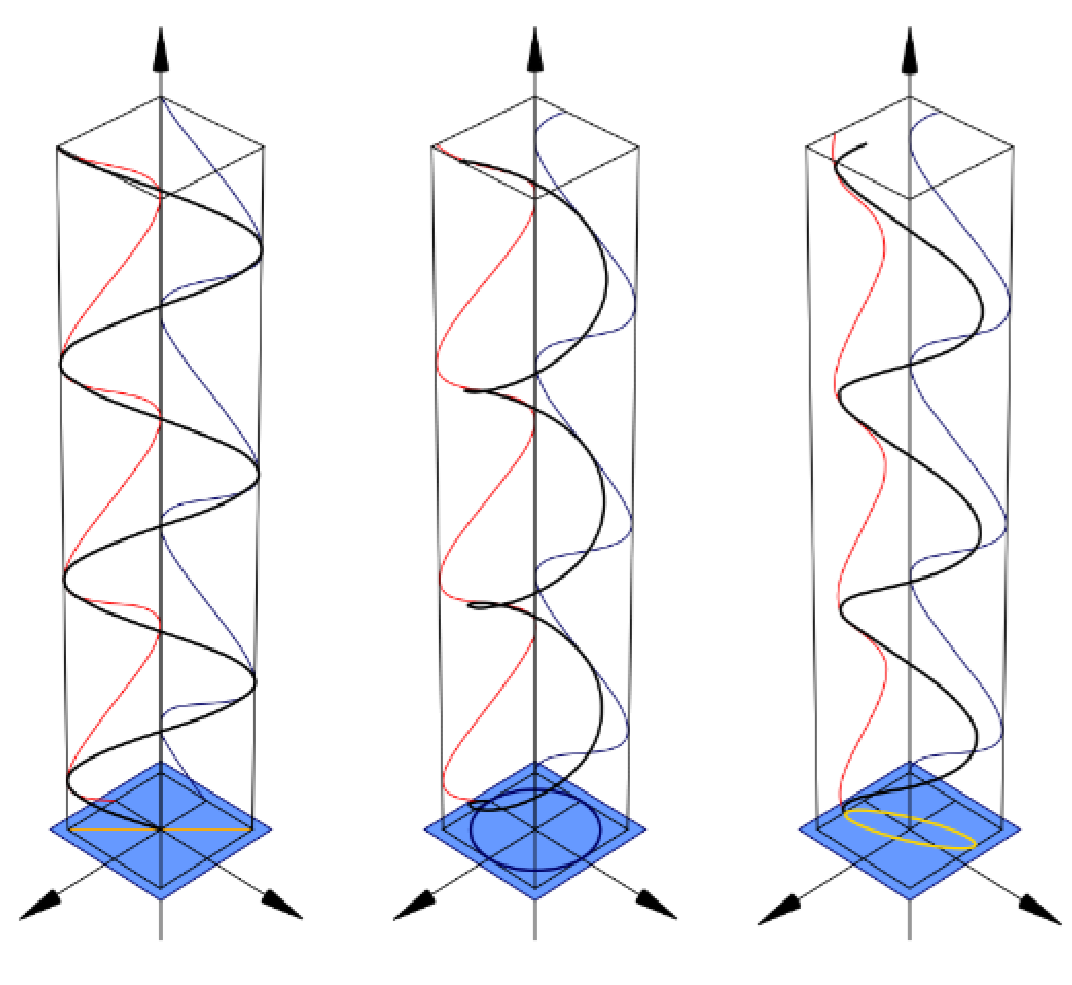
결론적으로 위상차의 크기에 따라 편광상태는 다음과 같은 모양을 한다.

4. 무편광 (unpolarized)
사실 자연에 존재하는 빛은 거의 incoherent 하다. 다시 말해서 위상차가 일정하지 않고, 시간에 따라 계속 무작위적으로 변한다. 따라서 이런 빛들은 무편광(unpolarized) 혹은 무작위 편광상태 (randomly polarized) 에 있다고 한다. 반대로 얘기하면 완전한 단색광 평면파 (monochromatic plane wave)는 항상 한 편광상태를 가지고 있다고 말할 수 있다. LASER와 LED등이 여기에 속한다.
자연에서도 가끔 부분편광을 가지고 있는 경우를 발견할 수 있는데, 반사하는 빛을 측정할 때, Brewster angle에서 부분편광을 관측할 수 있다.

