1. 비주기 파동
Frequency spectrum에서 임의의 공간주파수 $k_p$ 1개가 있다고 가정해보자. Frequency spectrum은 조화 파동의 주파수 별 진폭을 나타내는 그래프이기 때문에, 이 경우 그냥 조화파동일 것이다. 그런데 $k_p$를 중심으로 대칭되는 주파수 성분이 존재한다면 파동은 packet모양을 가지게 되고, 대칭되는 성분의 숫자가 늘어날 수록 파동 packet의 간격이 늘어나게 된다. 최종적으로 일정한 주파수 범위 내에서 연속적인 성분을 가지게 되면 (즉, 정규분포 꼴) 파동 packet의 주기가 늘어나다가 하나의 packet인 pulse 형태를 가지게 된다.

Fourier serise를 전개해 펄스 형태 파동을 주파수 분해하여 Fourier integral을 얻을 수 있다.
$$ f(x) = \frac{1}{\pi} [\int_{0}^{\infty} A(k)cos(kx) dk + \int_{0}^{\infty} B(k) sin(kx) dk] $$
$$ A(k) = \int_{-\infty}^{\infty} f(x)cos(kx)dx, \quad B(k) = \int_{-\infty}^{\infty} f(x) sin(kx) dx $$
$+L$ 부터 $-L$까지의 cosine 펄스 $(E=E_0 cos(k_p x))$ 에 대해서 Fourier integral을 수행하면,
$$ A(k) = E_0L[sinc(k_p-k)L + sinc(k_p+k)L] $$
로 주어진다. 잘 알고있겠지만, $sinc(x) = \frac{sin(x)}{x} $이다. 이 train에 많은 wave가 있을 때, 즉, $\lambda_p<<L ,k_pL>>2\pi$라면 $(k_p+k)>>2\pi$ 이다. $k$ 를 양수로만 제한한다면, 우리는 $A(k)$를다음과 같이 다시 쓸 수 있다.
$$ A(k) = E_0Lsinc(k_p-k)L$$
이 때 펄스폭 $\Delta x= 2L$, 주파수폭 $\Delta k = 2\pi/L$ 이다. 두 값을 곱하면 $\Delta k \Delta x = 4\pi$ 고, 이는 후에 양자역학에서 불확정성원리를 추론하는 바탕이 된다.
2. Fourier Filter
앞선 20. Superposition of Waves (2) 글에서 그려본 비조화 주기 파동 그래프를 보면, 고주파수 성분을 포함하면 할수록가장자리의 변화폭이 커지면서 경계가 뚜렷해지는것을 확인할 수 있다. 이미지에서 명암의 변화를 기준으로 Fourier transform을 수행하여 다시 이미지를 재구성 할 수 있는데, 이 때 고주파 성분을 저주파수 성분 대비 상대적으로 증폭시키면 원래 이미지의 가장자리를 보다 선명하게 만들 수 있다. 반대로 고주파 성분을 제거하면 그림이 뿌옇게 되며 blur 효과를 얻을 수 있다. 이렇게 이미지를 변경시키는 것을 Fourier filter라고 한다.



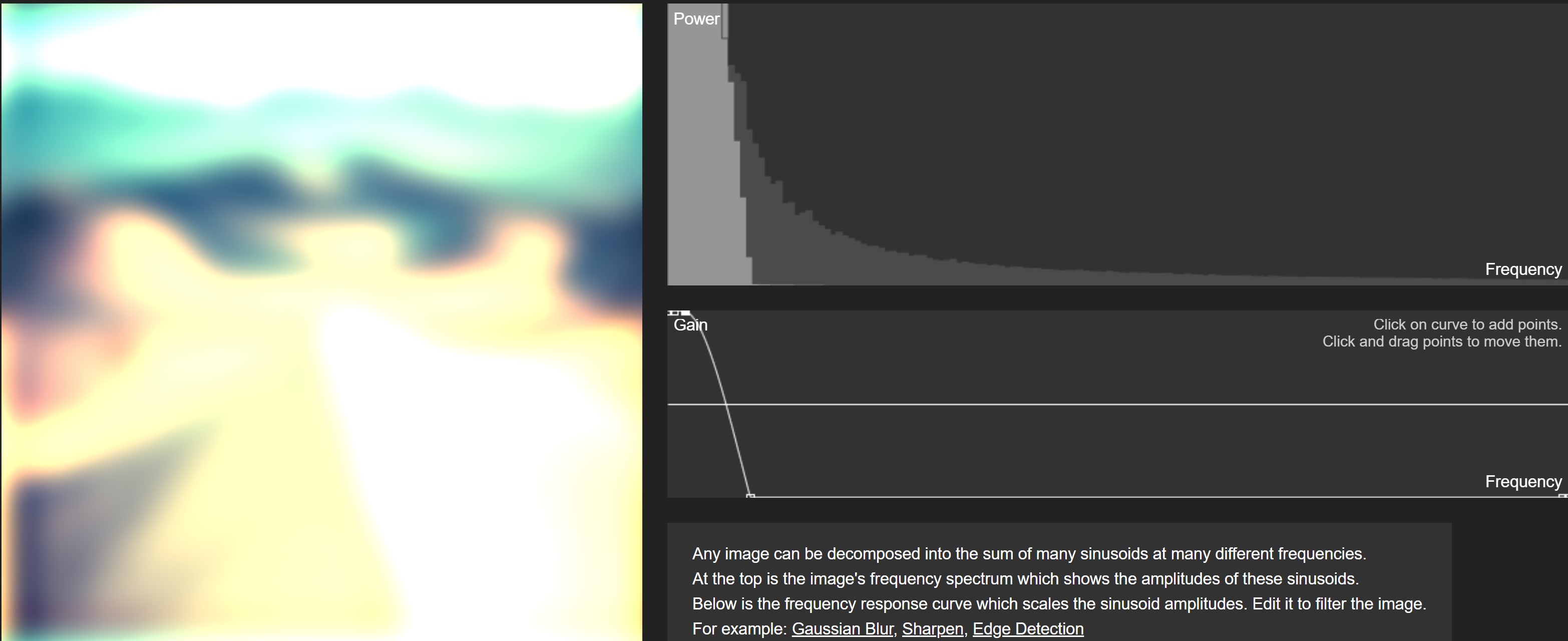
Fourier Filter는 다음 웹페이지에서 쉽게 체험해 볼 수 있다.
Fourier Image Filtering
Gain Frequency Click on curve to add points. Click and drag points to move them. Any image can be decomposed into the sum of many sinusoids at many different frequencies. At the top is the image's frequency spectrum which shows the amplitudes of these sinu
david.li
