지난 시간까지 Propagation of Light라는 제목으로 빛이 매질 속을 진행하며 발생하는 다양한 상호작용 현상에 대해 공부했다. 그렇지만 실제 구체적인 값을 얻을 수는 없었다. 따라서 우리는 electromagnetic approach를 통해, 즉 Maxwell equation과 그 경계조건을 이용해 빛의 상호작용을 조금 더 수식적으로, 구체적으로 이해해보려고 한다.
먼저 다음과 같은 네 가지 (전기장과 자기장 각각 두 가지) 경계조건을 잘 기억해야 한다.
| *Boundary Condition* i) 경계면에 평행한 전기장 혹은 자기장 성분은 경계면에서 연속적이다. ii) 경계면에 수직한 전기장 혹은 자기장 성분은 경계면에서 연속적이다. |
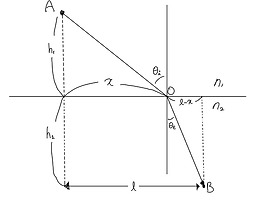
자 이제 다음과 같이 전자기파가 (즉, 빛이) 1번 매질에서 2번 매질로 진행하고 있다고 생각해보자.
전기장은 모니터로부터 나오는 방향으로, 자기장은 표시된 방향으로 나오며 각각 $\hat{k}$ 방향으로 진행하고 있다고 가정하자. 또 $\vec E$ 는 boundary surface에 평행하며 tangential한 방향의 성분만 갖는다. $\vec H$는 두 성분을 모두 갖는다. 그림과 같은 Free space(i.e., $\rho_f = 0, J_f =0$)에서, boundary condition과 Maxwell equation을 같이 쓰면 다음과 같다.
$$ \left\{\begin{matrix} \nabla \cdot \vec E = 0 \ , \quad \quad \ \hat n \cdot (\varepsilon_2 \vec E_2 -\varepsilon_1\vec E_1) = 0
\\ \nabla \times \vec E = -\frac{\partial \vec B}{\partial t} \ , \quad \quad \ \hat n \times (\vec E_2 -\vec E_1) = 0
\\ \nabla \cdot \vec B = 0 \ , \quad \quad \ \hat n \cdot (\vec B_2 -\vec B_1) = 0
\\ \nabla \times \vec B = \mu \varepsilon \frac{\partial \vec E}{\partial t} \ , \quad \quad \ \hat n \times (\frac{1}{\mu_2} \vec B_2 -\frac{1}{\mu_1} \vec B_1) = 0
\end{matrix}\right. $$
Boundary condition를 정리하면,
$$ \left\{\begin{matrix} \nabla \cdot \vec E = 0 \ , \quad \quad \ \varepsilon_2 \vec E_{2n} -\varepsilon_1\vec E_{1n} = 0
\\ \nabla \times \vec E = -\frac{\partial \vec B}{\partial t} \ , \quad \quad \ \vec E_{2t} -\vec E_{1t} = 0
\\ \nabla \cdot \vec B = 0 \ , \quad \quad \ \vec B_{2n} -\vec B_{1n} = 0
\\ \nabla \times \vec B = \mu \varepsilon \frac{\partial \vec E}{\partial t} \ , \quad \quad \ \frac{1}{\mu_2} \vec B_{2t} -\frac{1}{\mu_1} \vec B_{1t} = 0
\end{matrix}\right. $$
이제 경계조건을 한 개씩 살펴보자.
1. 처음에 언급한 것 처럼 $\vec E$는 tangential한 성분만 갖기 때문에, $\vec E_{1n} = \vec E_{2n} = 0$ 이다.
2. 두 번째 경계조건에서, $\vec E_{1t} = \vec E_{2t}$ 이므로
$$ [\vec E_i + \vec E_r ] _t = [\vec E_{t}]_t \\ \to E_i + E_r = E_t $$
3. 세 번째 경계조건에서, $ B_{1n} = B_{2n} $
4. 마지막 경계조건에서, $ \frac{1}{\mu_1} \vec B_{1t} = \frac{1}{\mu_2} \vec B_{2t} $ 이다.
이 때 자기장의 tangential 한 성분은 각각 $H_{it} = -H_i cos\theta_i$ ,$H_{rt} = H_r cos\theta_r$, $H_{tt} = -H_t cos\theta_t$ 이다. 따라서
$$ \frac{1}{\mu_1} (-B_i sin\theta_i + B_r sin\theta_r) = \frac{1}{\mu_2}(-B_t cos\theta _t) $$
한편 $ \vec E = E_0 e^{i(kz-\omega t)}, \vec B = B_0 e^{i(kz-\omega t)} $라고 하면
$$ \nabla \times \vec{E} = -ik(-E_y \hat{x} + E_x \hat{y}) = -\frac{\partial \vec B}{\partial t} = i\omega \vec B \\ \therefore \vec B = \frac{k}{\omega} \hat{z} \times \vec E = \frac{1}{v} \hat{z} \times \vec E$$
따라서 $ \left | \vec B \right | = \frac{1}{v} \left | \vec E \right | $ 이므로 $B_t = \frac{1}{v} E = \sqrt{\mu \epsilon} E$ 이다. 이를 대입하면
$$ \frac{1}{\mu_1} [-\sqrt{\mu_1 \epsilon_1} E_i cos\theta_i + \sqrt{\mu_1 \epsilon_1} E_r cos\theta_r ] = \frac{1}{mu_2} [-\sqrt{\mu_2 \epsilon_2} E_t cos\theta_t] \\ - \sqrt{\frac{\epsilon_1}{\mu_1}} E_i cos\theta_i + \sqrt{\frac{\epsilon_1}{\mu_1}} E_r cos\theta_r = - \sqrt{\frac{\epsilon_2}{\mu_2}} E_t cos\theta_t $$
여기까지 유도할 수 있다. 여기에 반사법칙 $(\theta_i = \theta_r)$과 굴절법칙$(n_1 sin\theta_i = n_2 sin \theta_t)$을 이용해서 두번째와 네번재 경계조건에서 얻은 식을 정리해보면 다음과 같다.
$$ 1. \quad E_i + E_r = E_t \to 1+ (\frac{E_r}{E_i}) = \frac{E_t}{E_i} $$
$$ 2. \quad \sqrt{\frac{\epsilon_1}{\mu_1}} E_i cos\theta_i - \sqrt{\frac{\epsilon_1}{\mu_1}}E_r cos\theta_r = \sqrt{\frac{\epsilon_2}{\mu_2}} E_t cos\theta_t \\ \to \ \sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i - \sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i {\frac{E_r}{E_i}} = \sqrt{\frac{\epsilon_2}{\mu_1}} cos\theta_t (\frac{E_t}{E_i})$$
이제 위 식을 정리해서 우리는 $ (\frac{E_r}{E_i})_{\perp} $ , $(\frac{E_t}{E_i})_{\perp}$ 를 구하려고 한다. 이 두 변수는 각각 반사계수와 투과계수 (혹은 굴절계수) 이다. $ \frac{E_r}{E_i} \equiv x$로 $\frac{E_t}{E_i} \equiv y$ 로 정의하고 위에서 얻은 두 식을 정리하면
$$ 1. \quad 1+x =y \\ 2. \quad \sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i - \sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i x = \sqrt{\frac{\epsilon_2}{\mu_2}} cos\theta_t y$$
$$ \rightarrow \quad x = (\frac{E_r}{E_i})_{\perp} = \frac{\sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i - \sqrt{\frac{\epsilon_2}{\mu_2}}cos\theta_t}{cos\theta_t \sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i + \sqrt{\frac{\epsilon_2}{\mu_2}} cos\theta_t} \\ \quad y = (\frac{E_t}{E_i})_{\perp} \frac{2\sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i}{\sqrt{\frac{\epsilon_1}{\mu_1}}cos\theta_i+\sqrt{\frac{\epsilon_2}{\mu_2}}cos\theta_t} $$
이제 거의 다 왔다. 분자 분모에 $\mu_1 \mu_2$를 곱해주고 $\cos \theta_t = \sqrt{1-(\frac{n_1}{n_2})^2 (sin\theta_i) ^2}$를 대입하면,
$$ (\frac{E_r}{E_i})_{\perp} = \frac{\mu_2 n_1 cos \theta_i - \mu_1 n_2 \sqrt{1-(\frac{n_1}{n_2})^2 sin\theta_i ^2}}{\mu_2 n_1 cos\theta_i + \mu_1 n_2 \sqrt{1-(\frac{n_1}{n_2})^2 sin\theta_i ^2}} \\ (\frac{E_t}{E_i})_\perp = \frac{2 \mu_2 n_1 cos\theta_i}{\mu_2 n_1 cos\theta_i + \mu_1 n_2 \sqrt{1-(\frac{n_1}{n_2})^2 sin \theta_i ^2}} $$
Fresnel equations 중 두 가지를 구했다.
위에서 구한것과 비슷한 방식으로 $\vec H$ 가 모니터에서 나오고, $\vec E$가 $\hat{n}, \hat{t}$ 방향을 모두 갖는 경우도 생각해 볼 수 있다. 이 경우도 마찬가지로 Maxwell equation과 boundary condition을 이용해 유도할 수 있다.
(작성중)
--
다음 게시글에서는 Fresnel Equations의 의미를 알아본다.
