이번 게시글에서는 금속에서 빛의 성질을 알아본다. 유전체에서는 각각 원자들이 점광원이 되어 radiation하는 과정을 통해 빛이 진행한다. 또, 우리는 유전체에서 빛의 진행을 알아볼 때 Free space라고 간주하고 Maxwell equation을 풀어 그 과정을 이해했다. 그러나 금속에서는 자유전자가 있어 국소적으로 전하밀도 $\sigma$ 가 0이 되지 않는다. Maxwell 방정식에서 이를 고려하면
$$ \nabla^2 \vec{E} = \mu \epsilon \frac{\partial^2 \vec E}{\partial t^2} + \mu \sigma \frac{\partial \vec{E}}{\partial t} $$
즉, $\mu \sigma \frac{\partial \vec{E}}{\partial t} $ 가 감쇄역할을 하게 된다. 자유전자는 전기장의 방향으로 운동을 하며 입사된 전자기파 에너지를 radiation 하지만, 다른 전자와 부딪혀 에너지를 잃고 열에너지로 방출한다. 금속 내부에서 전자기파의 전파를 알아보기 위해 우리는 복소굴절율 $\tilde {n}$을 정의한다.
$$ \tilde{n} = n_R - i n_I $$
$x$ 방향으로 전파하는 전자기파는
$$ \vec{E} = \vec{E_0} cos (\omega t -kx) \\ \rightarrow \vec{E} = \vec{E_0} e^{-\omega n_I x /c} cos \omega (t-n_R x/c) $$
따라서 빛의 세기는 $ I= I_0 e^{-\alpha x} $가 된다. 이 때 $\alpha \equiv 2\omega n_I /c $를 attenuation coefficient 라고 한다. 전파는 금속표면으로부터 $x=1/\alpha$의 거리를 지나면 $e^{-1} = 1/2.7 \approx \frac{1}{3} $ 으로 떨어진다. 즉, 이 거리만큼밖에 침투하지 못하고 흡수되며 내부에서 전파하지 못하게 된다. 이 거리를 skin depth라고 한다. 구리를 예로 들어보면, 100nm 정도의 파장을 갖는 UV빛은 약 0.6nm, 10000nm파장의 적외선에서는 6nm정도 skin depth를 갖기 때문에 전파가 내부까지 진행하지 못한다. 따라서 backward방향의 전자기파는 cancel되지 못하며, 따라서 매우 높은 반사율 $R$을 갖는다. 수직입사의 경우,
$$ R = (\frac{\tilde n - 1}{\tilde n + 1})(\frac{\tilde n - 1}{\tilde n + 1})^* = \frac{(n_R -1)^2 + n_I ^2}{(n_R +1)^2 + n_I ^2} $$
예시로 주석(tin)을 들어보자. 589.3nm 파장이 들어올 때 $n_R = 1.5, n_I = 5.3$ 이면, 반사율 $R=0.8$ 이다. 나트륨(sodium)의 경우, $n_R = 0.04, n_I =2.4$ 이므로, 반사율 $R= 0.9$ 인 것을 알 수 있다.
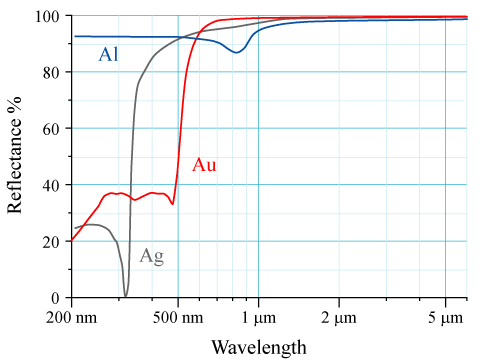
금, 은, 구리, 알루미늄 등의 금속은 UV (Ultra violet)이나 가시광선 이상의 파장영역에서 매우 높은 반사율을 가지며, cutoff가 일어나는 파장에 따라 색깔을 가지게 된다. 특히 알루미늄(aluminium)과 주석(tin), 강철(steel) 등을 전 파장에 걸쳐 높은 반사율을 갖기 때문에 거의 색이 없다. (즉, 은색으로 반짝거린다.)

Salar de Uyuni - 우유니 소금사막 By Christopher Crouzet - Own work, also available on Flickr, CC BY-SA 4.0, Link
한 편 dispersion equation (분산방정식, 유도과정) $n^2(\omega) = 1+ \frac{q^2 N}{\epsilon_0 m_e (\omega_0 ^2 - \omega^2)} $ 에서 $\omega >> \omega_0 $ 이면 위상이 $180^{\circ}$ 바뀐다는 것을 우리는 알고 있다. 그런데 금속에 있는 자유전자는 복원력이 없다. 즉, $\omega_0 ^2 = \frac{k}{m} = 0$ 이므로 모든 $\omega$ 에 대해서 위상이 180도 뒤집어지게 된다.



